یکی از مشکلات عمده دانشجویان در درس ریاضی مبحث انتگرال و انتگرال چندگانه هستش که خیلی از بچه ها به دلیل سختی، این مبحث رو نمیخونن اما همیشه این درس گریبان گیر تمام بچه های مهندسی هست.
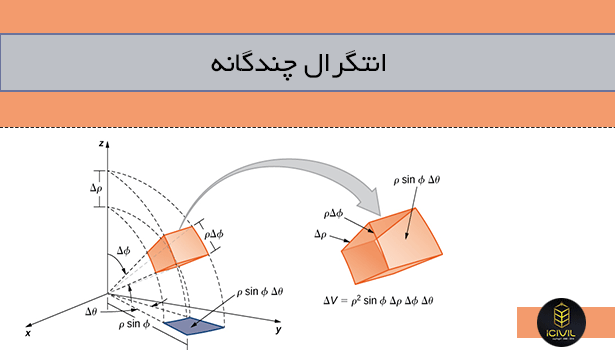
در این مطلب میخوایم انتگرال چندگانه رو با هم یاد بگیریم، بعد از خواندن این مطلب، متوجه میشید که مبحث سختی نیست.
۱-انتگرال دوگانه:
تعریف: فرض کنیم![]() یک ناحیه ی بسته و کران دار باشد و f روی D کران دار باشد، برای سادگی فرض کنیم که D یک مستطیل است.
یک ناحیه ی بسته و کران دار باشد و f روی D کران دار باشد، برای سادگی فرض کنیم که D یک مستطیل است.
![]()
یک افراز مانند P برای D برابر حاصلضرب افراز های P1 و P2 برای [a,b] و [c,d] است.
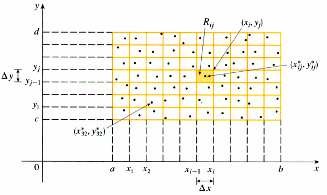
![]()


انتگرال بالایی f روی D را به صورت زیر تعریف می کنیم.
اگر نقطه دلخواه ![]() را در هر Rij انتخاب کنیم، آنگاه می توانیم هر قسمت از رویه را که بالاب Rij قرار دارد به صورت مکعب مستطیل های باریکی در نظر بگیریم مطابق شکل زیر قرار میدهیم.
را در هر Rij انتخاب کنیم، آنگاه می توانیم هر قسمت از رویه را که بالاب Rij قرار دارد به صورت مکعب مستطیل های باریکی در نظر بگیریم مطابق شکل زیر قرار میدهیم.
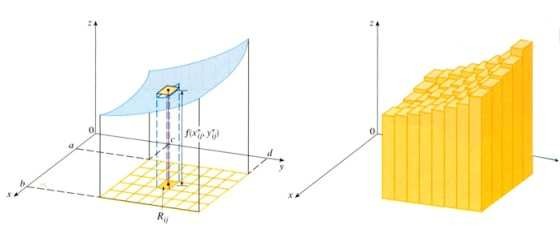

که در آن (S(p,f مجموع حجم مکعب مستطیل می باشد.
تعریف: اگر ![]() موجود و متناهی باشد آن مقدار حد را انتگرال دوگانه f روی D نامیده و به صورت
موجود و متناهی باشد آن مقدار حد را انتگرال دوگانه f روی D نامیده و به صورت
![]()
نشان می دهیم.

و انتگرال پایینی f روی D مشابهاً به صورت زیر تعریف میشود.
![]()
تعریف: اگر آنگاه f را روی D انتگرال پذیر می نامیم و انتگرال f روی D به صورت های زیر نشان میدهیم.
اگر ![]() یک جعبه n بعدی باشد، آنگاه;
یک جعبه n بعدی باشد، آنگاه;
![]()
و f روی D کران دار باشد آن گاه انتگرال f روی D مشابه فوق تعریف میشود، و به صورت![]() نشان داده میشود.
نشان داده میشود.
اگر ![]() آنگاه:
آنگاه:
![]()
نکته: اگر ![]() بسته و گران دار دلخواه باشد و چون D کران دار است پس در یک جعبه n بعدی مانند
بسته و گران دار دلخواه باشد و چون D کران دار است پس در یک جعبه n بعدی مانند![]() جای دارد.
جای دارد.

تعریف میکنیم.

و

قضیه: اگر تابع f روی ناحیه ی بسته و کران دار D در R^n پیوسته باشد آنگاه f روی D انتگرال پذیر است.
بنابراین در این درس همواره فرض بر این است که f پیوسته باشد لذا نیازی به بررسی انتگرال پذیری نمی باشد فقط روش های محاسبه ی انتگرال مورد نظر می باشد.
خواص انتگرال چند گانه
فرض کنید ![]() بسته و کران دار باشد و f و g روی D انتگرال پذیر باشند، آنگاه:
بسته و کران دار باشد و f و g روی D انتگرال پذیر باشند، آنگاه:
۱) ![]()
۲)اگر ![]() برای هر
برای هر ![]() آنگاه
آنگاه
![]()
۳) ![]() برای هر عدد حقیقی a.
برای هر عدد حقیقی a.
۴) ![]() که در آن µ(D) اندازه D است.
که در آن µ(D) اندازه D است.
(اگر![]() باشد آنگاه µ(D) برابر طول D است، اگر
باشد آنگاه µ(D) برابر طول D است، اگر![]() باشد آنگاه µ(D) مساحت D است اگر
باشد آنگاه µ(D) مساحت D است اگر![]() آنگاه µ(D) برابر حجم D است.)
آنگاه µ(D) برابر حجم D است.)
۵) اگر![]() به طوری که
به طوری که![]() (میتوانند مرز مشترک داشته باشند) وقتی که
(میتوانند مرز مشترک داشته باشند) وقتی که![]() در این صورت انتگرال روی اجتماع برابر است با:
در این صورت انتگرال روی اجتماع برابر است با:
![]()
۶) اگر![]() و
و ![]() برای هر
برای هر ![]() آنگاه
آنگاه ![]() برابر است با حجم ناحیه ی محدود بین رویه ی
برابر است با حجم ناحیه ی محدود بین رویه ی ![]() و D.
و D.
(انتگرال دوگانه همواره حجم نمی دهد اما اگر![]() باشد آنگاه حجم را محاسبه میکند.)
باشد آنگاه حجم را محاسبه میکند.)
۷) تعبیر کلی (کاربرد) برای انتگرال های n گانه به صورت زیر است:
اگر تابع f مشخص کننده ی چگالی ماده ای در هر نقطه از جسم D باشد آنگاه ![]() مشخص کننده ی کل ماده ی موجود در جسم D است.
مشخص کننده ی کل ماده ی موجود در جسم D است.

۹) اگر f روی ناحیه ی بسته و کران دار ![]() پیوسته و کران دار باشد آنگاه نقطه ی
پیوسته و کران دار باشد آنگاه نقطه ی ![]() وجود دارد به طوری که:
وجود دارد به طوری که:
![]()
۱۰) میانگین تابع f روی D برابر است با

روش های محاسبه ی انتگرال های چند گانه:
الف)انتگرال دوگانه: برای محاسبه انتگرال ![]() براساس وضعیت ناحیه ی D چهار حالت داریم:
براساس وضعیت ناحیه ی D چهار حالت داریم:
۱) D یک مستطیل است.

برای محاسبه انتگرال نسبت به هر یک از متغیر ها، متغیر دیگر را ثابت در نظر میگیریم.
پرسش: آیا میتوان گفت  ؟
؟
در حالت کلی جواب منفی است ولی قضیه ی فوبینی مهم می باشد.
قضیه فوبینی: اگر f روی D پیوسته باشد آن گاه داریم:
![]()
برای ادامه یادگیری انتگرال چند گانه بر روی لینک دانلود راست کلیک کرده و گزینه save link as… را انتخاب کنید.













